Cálculo Integral

 

Una vez estudiado el concepto de derivada, pasaremos a estudiar el de primitiva de una función, que seguirá un procedimiento inverso.

Una función F(x) es la primitiva de f(x) en un intervalo I si se cumple que F'(x)=f(x) para cualquier punto x del intervalo I . Llamamos integral indefinida de f(x) en el intervalo I, al conjunto de todas las primitivas de f(x) en I .

Escribiremos :

donde C es una constante de integración.

Integrales inmediatas

Propiedades de la Integral

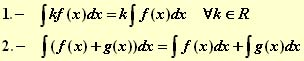
Cálculos Integrales

• Integral por sustitución
• Integral por partes
• Integral de funciones racionales
• Integral de funciones trigonométricas
• Aplicaciones de la integral

QUIÉN SOY | CONTACTO
                                         CONSULTAS:  4º ESO | 1º BACHILLERATO |2º BACHILLERATO | SELECTIVIDAD| LÍMITES | DERIVADAS | INTEGRALES | GRÁFICAS| CÓNICAS
                              CONSULTAS CON DERIVE: LÍMITES | DERIVADAS | GRÁFICAS