donde C(x) es el cociente y R(x) el resto.

Como C(x) es un polinomio, es facilmente integrable, y la complejidad del estudio estará en el cociente donde el grado de R(x) es menor que el de Q(x). Este último caso, será por tanto, el estudio que nos ocupará de ahora en adelante y lo desarrollaremos dependiendo de los grados:

1.- El grado del denominador es uno. En este caso el grado del numerador será uno, ya que éste tiene que ser menor que el del denominador:

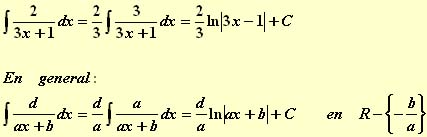
Veamos un ejemplo:

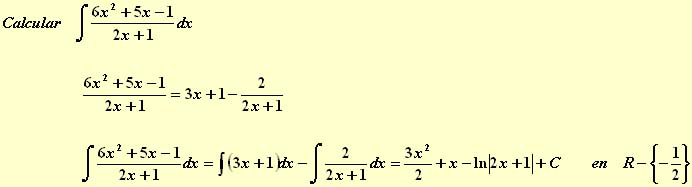
2.- El grado del numerador es uno y el del denominador es dos. Es decir, el grado de P(x) es uno y el grado de Q(x) es dos. Vamos a diferenciar dos casos:

• Q(x) tiene dos raices distintas y reales: Se resuelve por descomposición polinomica, si Q(x)=(x-a)(x-b) podemos escribir:

, ahora nos queda calcular A y B.

Veamos un ejemplo:

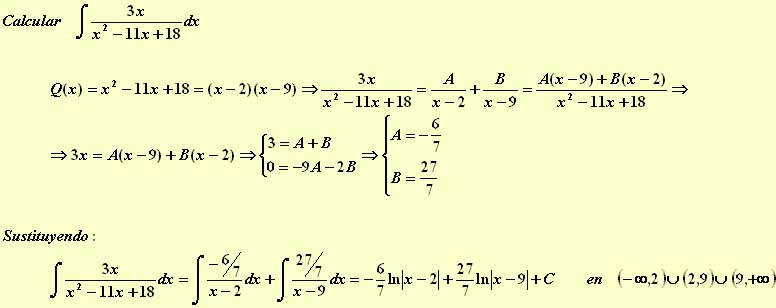
Veamos otro ejemplo:

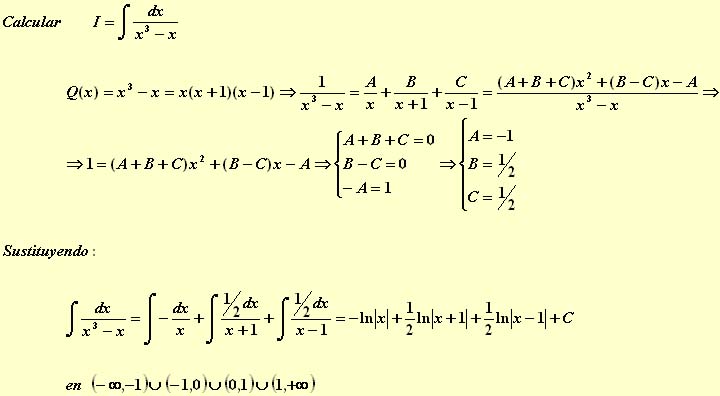
• Q(x) tiene las dos raices reales iguales. Tendríamos dos nuevos casos:

i.-

ii.-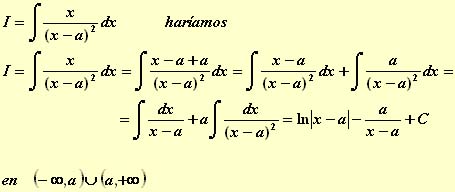

3.- El polinomio Q(x) no tiene raices reales. Este caso se resuelve completando cuadrados:

Después de sustituir quedan dos casos:

a.-

b.-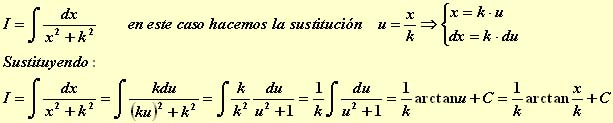

Ejemplo 1º

Ejemplo 2º

Problemas de descomposición polinómica

Problema 1º

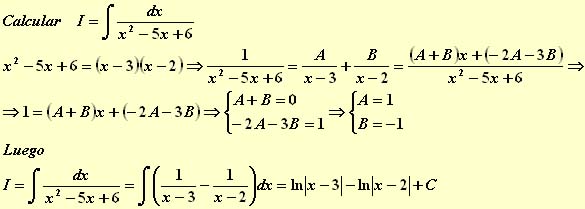
Problema 2º

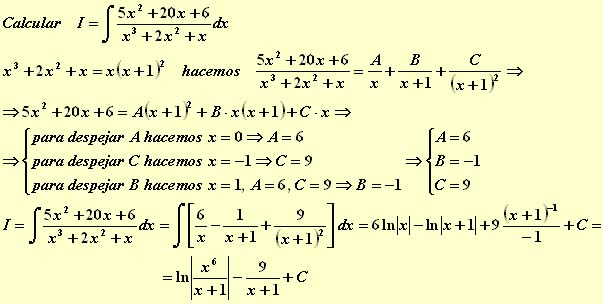
Problema 3º

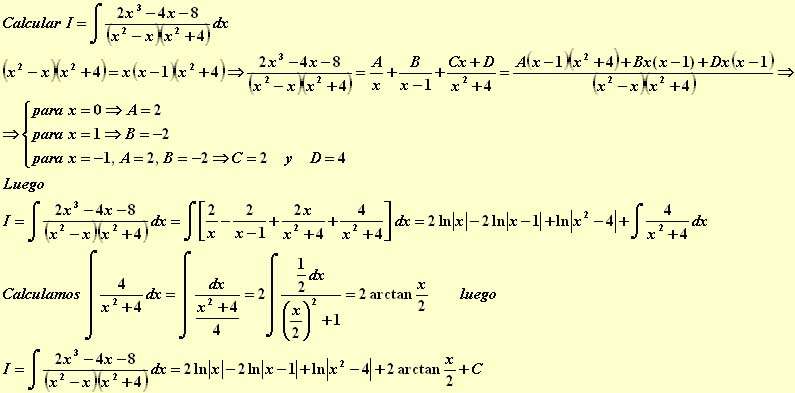
Problema 4º

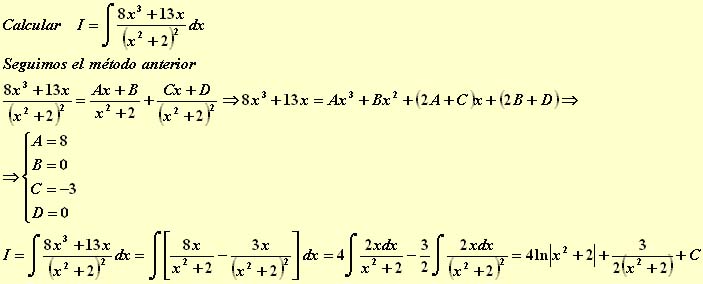
Problema 5º

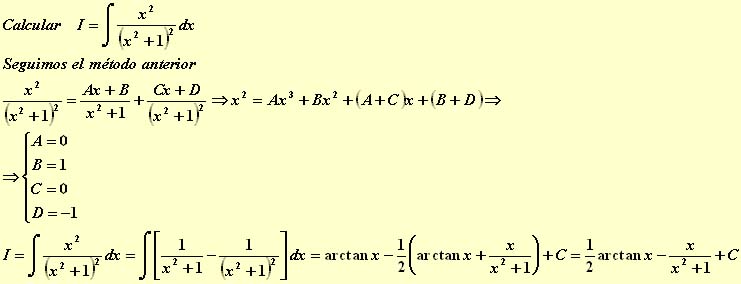
Inciso

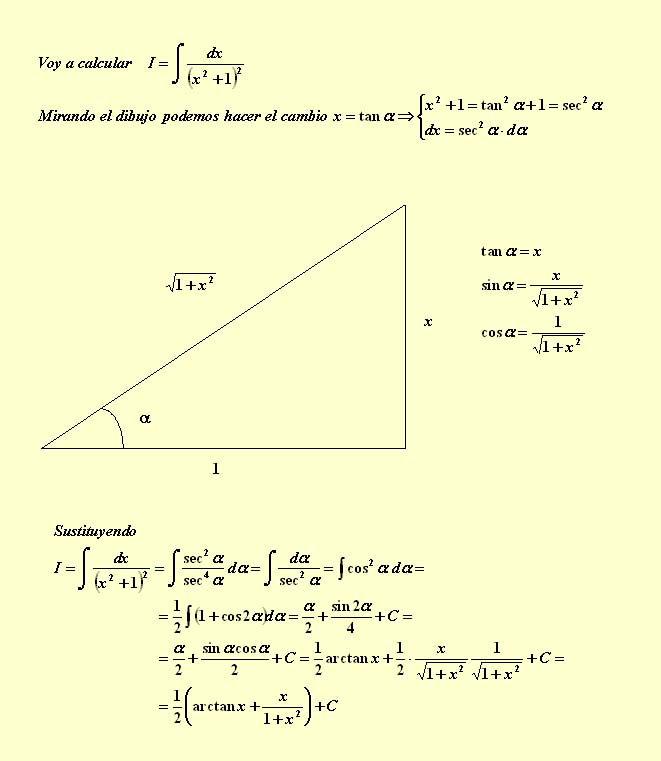
Problema 6º

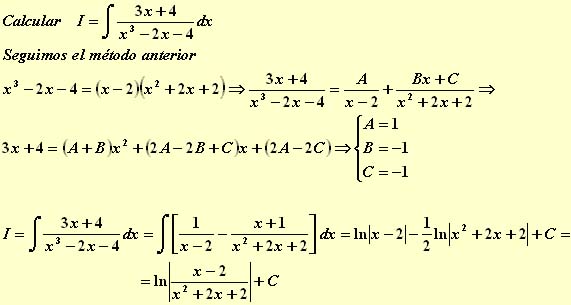
Ahora ha llegado la hora de entrenarse con algunos ejercicios que voy a proponer: PULSAR