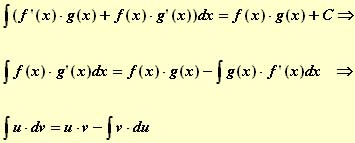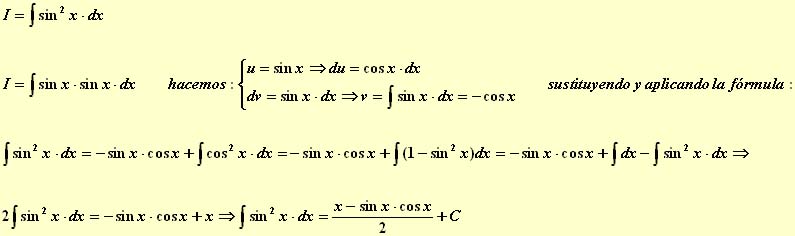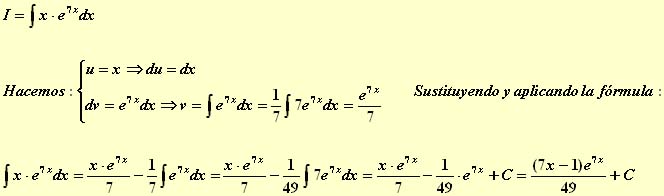Integral por partes

 

Si tenemos dos funciones derivables f y g en un intervalo I, podemos calcular la derivada producto:

[f(x)·g(x)]'=f'(x)·g(x)+f(x)·g'(x) para cualquier punto x del intervalo I.

Esto quiere decir que f'(x)·g(x)+f(x)·g'(x) es una primitiva de f(x)·g(x), por lo que podemos escribir:

Veamos unos ejemplos:

Ejemplo 1º Calcular:

Ejemplo 2º Calcular:

Ejemplo 3º Calcular:

 

Integrales que comúnmente se resuelven por partes

 

Ejercicios Resueltos

 

Para que te entrenes con este método te propongo que resuelvas alguno de los problemas que te dejo en esta página PULSAR