|
Elipse
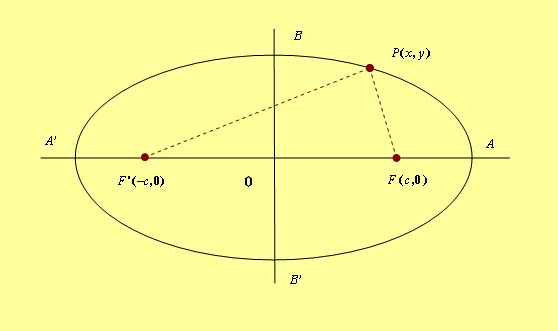
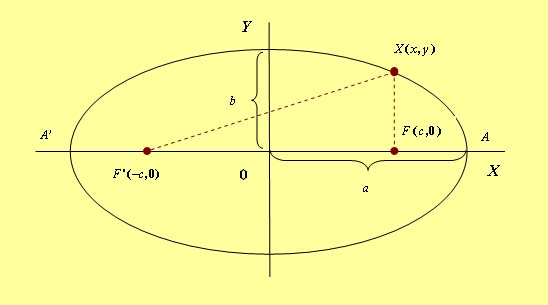
Es el lugar geométrico de los puntos tales que la suma de sus distancias a los focos es siempre constante e igual a 2a (longitud del eje mayor). A la vista del dibujo:
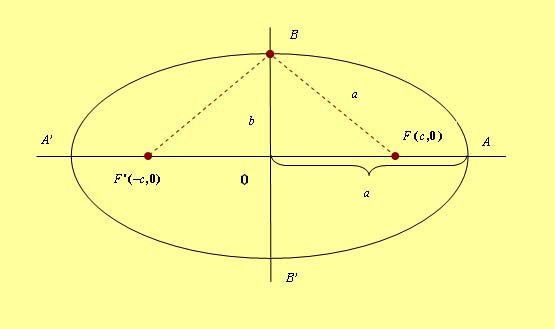
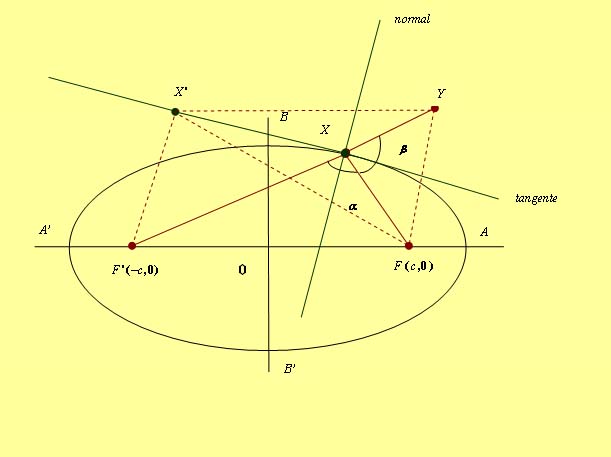
Relación fundamental Excentricidad Rectas tangentes y normales a una elipse en un punto Las rectas tangente y normal son la bisectrices de los ángulos que forman los radios vectores. Ecuación de la elipse Cuando los ejes coinciden con los ejes de coordenadas obtenemos la ecuación canónica de la elipse:
A partir de la ecuación canónica obtenemos la ecuación reducida
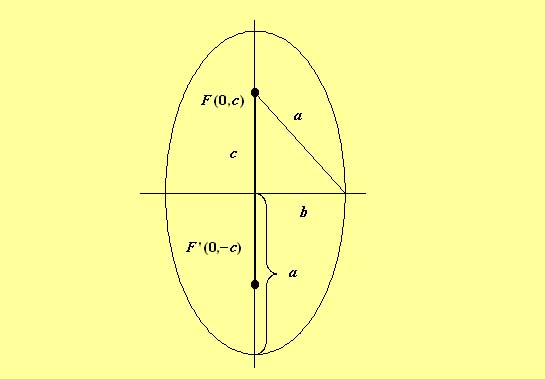
Vuelvo a recordar que estas ecuaciones son referentes a elipses cuyos ejes son coincidentes con los ejes de coordenadas En el caso de que la elipse no este centrada en el origen de coordenadas su ecuación canónica sería:
Para ver los ejemplos PULSAR Un poco mas complejo es cuando los ejes no coinciden con los ejes de coordenadas para ver un par de ejemplos PULSAR Unos ejemplos sobre cálculos de rectas tangentes y normales a la elipse PULSAR Ya sólo queda que te entrenes un poco: PULSAR
|