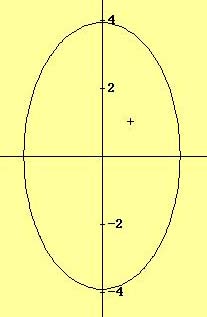
Ejemplos
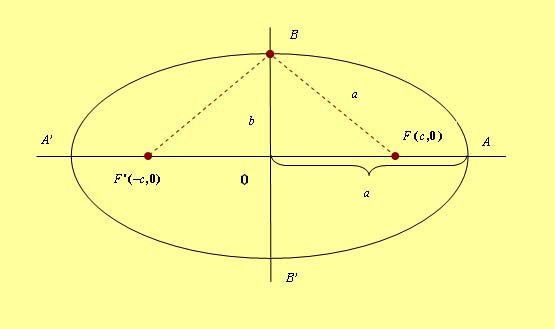
1.- La longitud del eje menor de una elipse es de 9u, y la distancia focal es de 12u. Calcular su excentricidad y su eje mayor.
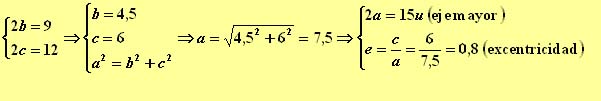
2.- La longitud del eje menor de una elipse 12u, y la del eje menor es de 20u. Calcular la distancia focal y su excentricidad.
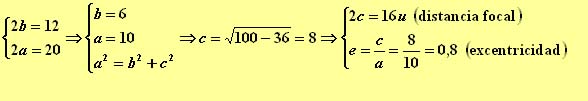
3.-La longitud del eje mayor de una elipse es de 20u, y su distancia focal es de 8u. Calcular su eje menor y su excentricidad.
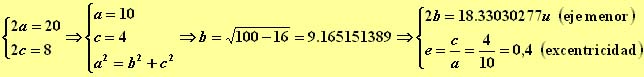
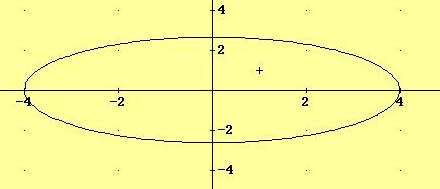
4.- Hallar la ecuación reducida de una elipse sabiendo que sus focos son F(3,0) y F'(-3,0), y que la suma de las distancias desde un punto cualquiera de la elipse a éstos vale 8. (2a=8, eje mayor que estaría sobre el eje de abcisas).
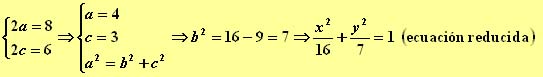
5.- Hallar la ecuación reducida de una elipse sabiendo que sus focos son F(0,3) y F'(0,-3), y que la suma de las distancias desde un punto cualquiera de la elipse a éstos vale 8. (2a=8, eje mayor que estaría sobre el eje de ordenadas).
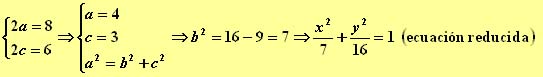
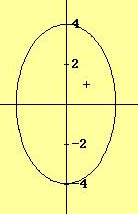
6.- Calcular la ecuación reducida de una elipse conociendo los vértices A'(-12,0), A(12,0) y su excentricidad e=0,6.
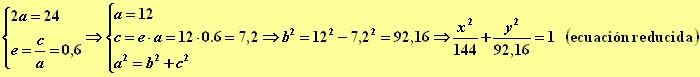
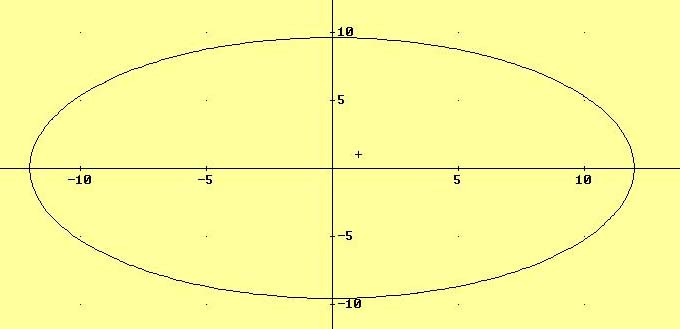
7.- Determinar los vértices, los focos y la excentricidad de la elipse ![]()
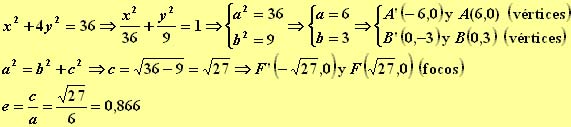
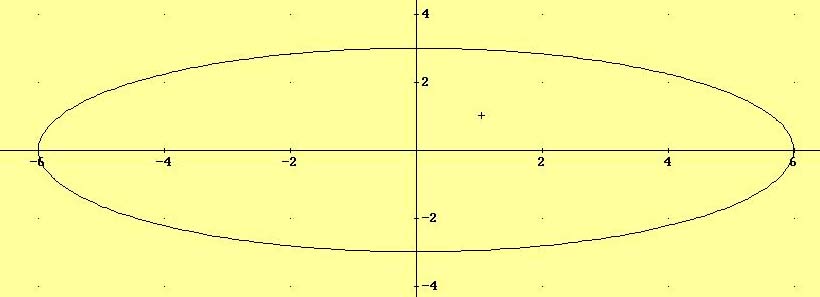
8.- Determinar los vértices, los focos y la excentricidad de la elipse ![]()
En este ejemplo el eje mayor esta situado sobre el eje de ordenadas:
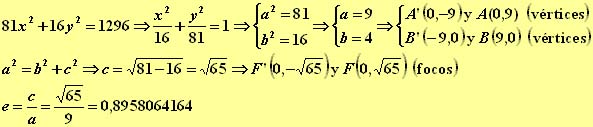
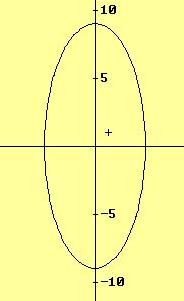
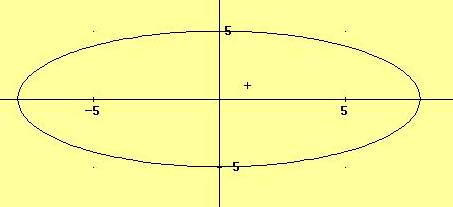
9.- Determinar los vértices, los focos y la excentricidad de la elipse ![]()
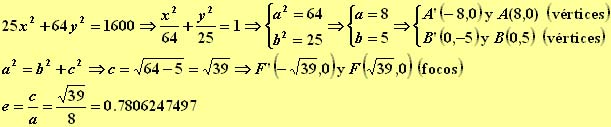
10.- Determinar los vértices, los focos y la excentricidad de la elipse ![]()
En este ejemplo el eje mayor esta situado sobre el eje de ordenadas:
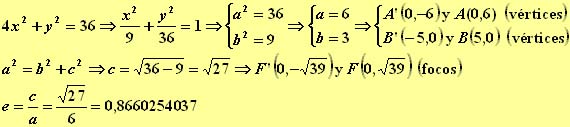
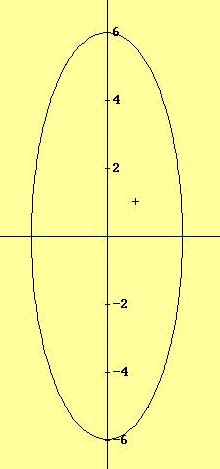
11.- Calcular la ecuación de una elipse que pase por los puntos (3,2) y (-1,-3). Calcular también la distancia focal y su excentricidad.

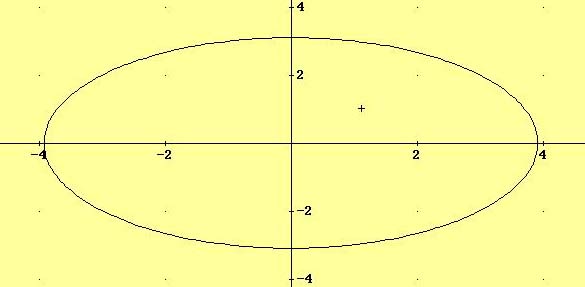
12.- Calcular la ecuación de una elipse que pase por los puntos (-3,-1) y (2,3). Calcular también la distancia focal y su excentricidad.