Decimos que una función f tiene un máximo relativo en un dominio D si en ese dominio existe un p de D de manera que f(p)>f(x) para cualquier x de D.
Decimos que una función f tiene un mínimo relativo en un dominio D si en ese dominio existe un p deD de manera que f(p)>f(x) para cualquier x de D.
Para calcularlos hacemos f'(x)=0 y todos los puntos que cumplan esta condición serán puntos críticos, es decir, en estos puntos la tangente a la gráfica es paralela al eje de abcisas. Para decidir si estos puntos son máximos, mínimos o de inflexión podemos utilizar dos métodos:
1. Utilizando el criterio de la segunda derivada: Supongamos que p es una solución de la ecuación f'(x)=0.
Si f''(p)>0 la función tiene un mínimo en el punto .
Si f''(p)<0 la función tiene un máximo en el punto .
Si f''(p)=0 la función tiene en un punto de inflexión (condición que se vio en el apartado anterior).
2. Comprobando el crecimiento y el decrecimiento a ambos lados del punto crítico: Supongamos que p es una solución de la ecuación f'(x)=0.
Si en el punto p pasamos de creciente a decreciente estamos ante un máximo.
Si en el punto p pasamos de decreciente a creciente estamos ante un mínimo.
Si en el punto p pasamos de creciente a creciente, o de decreciente a decreciente, estamos ante un punto de inflexión.
Este último método se suele utilizar cuando es muy laborioso calcular la segunda derivada.
Ejemplo:
Vamos a estudiar los puntos críticos de un ejemplo anterior por los dos métodos 
.
Teníamos que 
. Para decidir sobre ellos calculamos su segunda derivada:
f''(x)=6x-6
Si sustituimos x=3 tendremos f''(3)=18-6=12>0 Luego estamos ante un mínimo.
Si sustituimos x=-1 tendremos f''(-1)=-6-6=-12<0 Luego estamos ante un máximo.
En ese mismo ejemplo se veía que la función crecía en el intervalo
y decrecía en el (-1,3), es decir, que pasa en el punto x=-1 de creciente a decreciente, luego estamos ante un máximo. En el intervalo 
la función es creciente, luego en el punto x=3 la función pasa de decreciente a creciente y por tanto estamos ante un mínimo.
Veamos otra vez la gráfica:
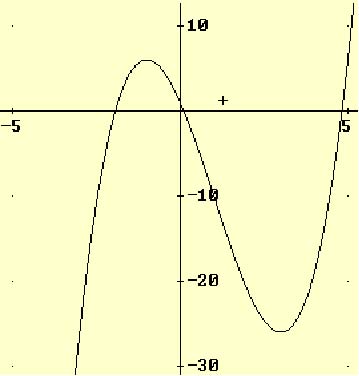
Resolvemos el ejemplo con Derive: PULSAR
