Ejemplo:

Dibujar la gráfica de

1. Hay varios apartados:
" Cortes con los ejes:

Si hacemos x=0 es f(0)=0. Es decir, la gráfica pasa por el punto (0,0).

Si hacemos f(x)=0 tenemos x=0 y x=4. Es decir la gráfica pasaría por los puntos (0,0) y (4,0)
" Dominio: Será todo R, la función existe para cualquier valor de x.
" Asíntotas:
1. Verticales: x=p es una asíntota vertical si . No hay ningún valor de que haga tender al función hacia infinito.
2. Horizontales: y=t es una asíntota horizontal si . Es decir, la función no tiene asíntotas horizontales.
3. Oblicuas: Si la recta y=ax+b es una asíntota de la función entonces

No existen asíntotas oblicuas.

" Simetrías: Comprobamos que . Es decir, la función no tiene simetrías.
2. Hay varios apartados:
" Puntos que anulen la primera derivada: . Luego los puntos en los que se anula la primera derivada son (0,0), (1,-27) y (4,0).
" Puntos que anulen la segunda derivada: Se anula en los puntos (2,-16) y (4,0) donde tendrá los puntos de inflexión.

3. Hay varios apartados:
" Si sustituimos el valor x=0 de en la segunda derivada tenemos f''(0)=96>0. Lo que nos quiere decir que estamos ante un mínimo. En x=4 ya hemos visto que se trata de un punto de inflexión. En x=1 tenemos f''(1)=36>0, por lo que estamos ante un mínimo.
" Para estudiar el crecimiento y decrecimiento de la función observamos que sólo es necesario estudiar el signo de (x-1). Luego la primera derivada será negativa si x<1 y positiva si x>1. En conclusión:
En el intervalo la función decrece, pues en este intervalo f'(x)<0.
En el intervalo la función crece, pues en este intervalo f'(x)>0.
Como se puede ver la función en el punto (1,-27) ha pasado de decrecer a crecer, lo que quiere decir que estamos ante un mínimo, como ya habíamos visto (¿más fácil que obtener la segunda derivada?). Se puede ver también que en el punto(2,-16) la función pasa de crecer a crecer, y en el (4,0) pasa igualmente de crecer a crecer, es decir, son puntos de inflexión como ya habíamos visto.
" Si observamos la segunda derivada vemos el siguiente diagrama

 

		(2,4)
x-2	-	+	+
x-4	-	-	+
f''(x)	+	-	+

Luego en el intervalo (2,4) la derivada segunda f''(x)<0, luego es Cóncava hacia abajo.
Y en los intervalos Ula derivada segunda f''(x)>0, luego es Cóncava hacia arriba.

4. Ahora ordenamos los resultados para dibujarlos:

Puntos de corte con los ejes: (0,0) y (4,0)
Dominio: Todo R

Asíntotas: No hay asíntotas
Crecimiento y decrecimiento: Decrece en Crece en
Concavidad: Cóncava hacia abajo en (2,4) Cóncava hacia arriba U
Dibujamos la gráfica:

 

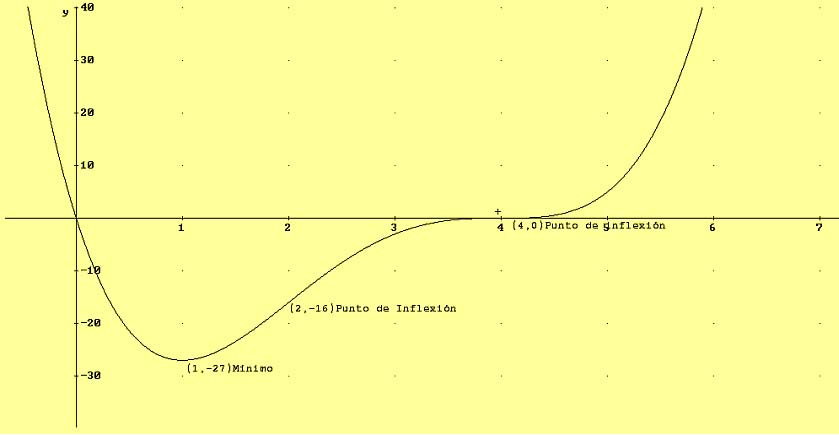
Resolvemos el ejemplo con Derive: PULSAR