Ejemplo:

Dibujar la gráfica de

1. Hay varios apartados:
" Cortes con los ejes: Si hacemos x=0 entonces f(0)=0. Es decir, la gráfica pasa por el punto (0,0). Si hacemos f(x)=0 entonces x=0. Es decir la gráfica sólo pasaría por el punto (0,0).
" Dominio: Será todo R, ya que el dominio del numerador es todo R, mientras que el denominador es siempre positivo y no se anula nunca
" Asíntotas:
1. Verticales: x=p es una asíntota vertical si . Esto quiere decir que, las únicas asíntotas posibles serían en aquellos puntos en los que se anulara el denominador, y como hemos visto no se anula nunca.

2. Horizontales: y=t es una asíntota horizontal si 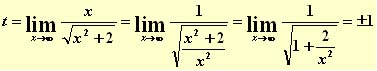. Es decir, la recta y=1 y la recta y=-1 son asíntotas horizontales.
3. Oblicuas: Una función que tiene asíntotas horizontales no tiene asíntotas oblicuas.

" Simetrías: Comprobamos que .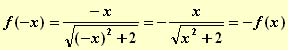
Es decir, la función es simétrica respecto al origen de coordenadas.

2. Hay varios apartados:
" Puntos que anulen la primera derivada: 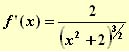. Luego no existe ningún punto que anule la primera derivada.
" Puntos que anulen la segunda derivada: 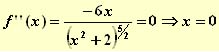Luego tiene un punto de inflexión en el (0,0).

3. Hay varios apartados:
" Como no hay puntos que anulen la primera derivada, no hay ni máximos ni mínimos.
El numerador y el denominador de la primera derivada son siempre positivos, luego la función es creciente en todo R.
Como se puede ver la función en el punto (0,0) ha pasado de crecer a crecer, lo que quiere decir que estamos ante un punto de inflexión, como ya habíamos visto (¿más fácil que obtener la segunda derivada?).
Si observamos la segunda derivada vemos que el denominador es siempre positivo, por lo que para estudiar la concavidad sólo tenemos que centrarnos en el numerador. El numerador es negativo si x>0, mientras que es positivo si x<0.

Luego en el intervalo la derivada segunda f''(x)>0, luego es Cóncava hacia arriba.
Y en los intervalos la derivada segunda f''(x)<0, luego es Cóncava hacia abajo.

4. Ahora ordenamos los resultados para dibujarlos:

Puntos de corte con los ejes: (0,0)

Dominio: R

Asíntotas: y=1, y=-1

Crecimiento y decrecimiento: Crece en todo R
Concavidad: Cóncava hacia abajo en Cóncava hacia arriba en

Dibujamos la gráfica:

 

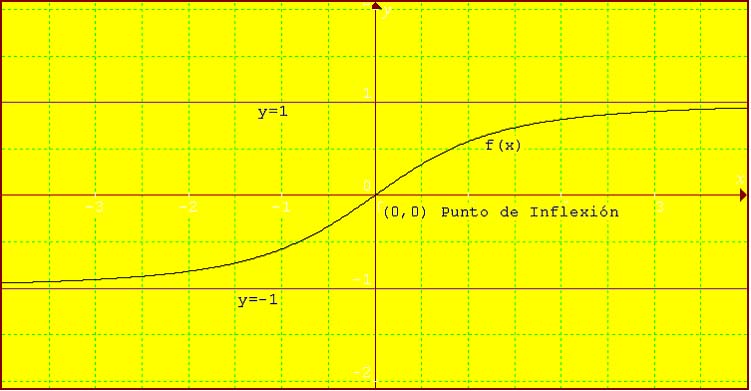
Resolvemos el ejemplo con Derive: PULSAR