Una función es creciente en un intervalo I si para todo x e y de I que satisfacen x<y se tiene que f(x)<f(y)
Una función es decreciente en un intervalo I si para todo x e y de I que satisfacen x<y se tiene que f(x)>f(y)
La forma más corriente de encontrar los intervalos de crecimiento y decrecimiento es a través de la primera derivada:
Una función es creciente en un intervalo I si para todo x de I se cumple que f'(x)>0
Una función es decreciente en un intervalo I si para todo x de I se cumple que f'(x)<0
Ejemplo:
Vamos a encontrar los intervalos de crecimiento y decrecimiento de la función 
1. La función es derivable en 
y su derivada será: 
2. 
3. Estudiamos el siguiente diagrama:
 |
(-1,3) |
 |
|
|
(x+1) |
- |
+ |
+ |
|
(x-3) |
- |
- |
+ |
|
f'(x)=(x+1)(x-3) |
+ |
- |
+ |
Podríamos concluir con que la función es creciente en el intervalo , decrece en el intervalo (-1,3) y vuelve a crecer en el intervalo .
Veamos un dibujo de la gráfica:
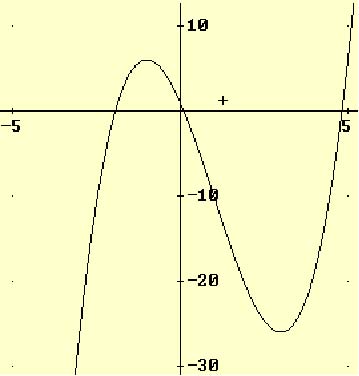
Resolvemos el ejemplo con Derive: PULSAR
