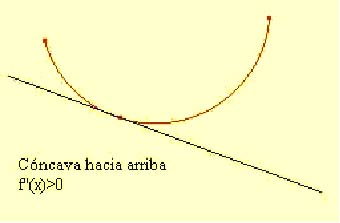
Sea f una función derivable en el punto p del intervalo I, diremos que f es cóncava hacia arriba en ese punto p si f''(p)>0, es decir, la tangente a la gráfica en ese punto está por debajo de ella. La función será cóncava hacia arriba en todo el intervalo si lo es en todo punto p de I.
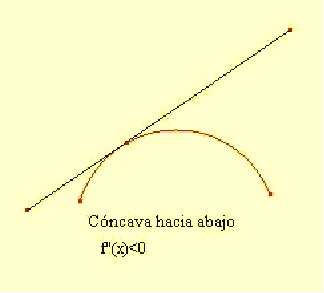
Sea f una función derivable en el punto p del intervalo I, diremos que f es cóncava hacia abajo en ese punto p si f''(p)<0, es decir, la tangente a la gráfica en ese punto está por encima de ella. La función será cóncava hacia abajo en todo el intervalo si lo es en todo punto p de I.
Sea f una función derivable en el punto p del intervalo I, diremos que tiene un punto de inflexión en p si f''(p)=0. Es decir, en ese punto ni es cóncava hacia arriba ni es cóncava hacia abajo.
La utilidad del estudio de la concavidad en las representaciones gráficas depende de la facilidad en el cálculo de la segunda derivada, así como en la cantidad de datos que nos puedan haber aportado otros estudios.
Ejemplo:
Vamos a estudiar la concavidad de la función 
Solución:
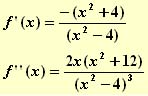
Ahora hay que estudiar en que intervalos la derivada segunda es positiva negativa o nula. Lo primero que vemos en la expresión es que
, esto quiere decir que no afecta al estudio del signo de la función. También nos damos cuenta que 
.
Ahora construimos el siguiente diagrama:
 |
(-2,0) |
(0,2) |
 |
|
|
x+2 |
- |
+ |
+ |
+ |
|
x |
- |
- |
+ |
+ |
|
x-2 |
- |
- |
- |
+ |
|
f''(x) |
- |
+ |
- |
+ |
En conclusión:
En el intervalo tenemos que f''(x)<0 y por tanto es cóncava hacia abajo.
En el intervalo (-2,0) tenemos que f''(x)>0 y por tanto es cóncava hacia arriba.
En el intervalo (0,2) tenemos que f''(x)<0 y por tanto es cóncava hacia abajo.
En el intervalo tenemos que f''(x)>0 y por tanto es cóncava hacia arriba.
En el punto x=0 tenemos que f''(x)=0 y por tanto es un punto de inflexión.
Veamos un dibujo de su gráfica:
Resolvemos el ejemplo con Derive: PULSAR
